[DL] 딥러닝을 위한 준비

딥러닝에 대해 본격적으로 알아보기 전에 머신러닝 내용에서 딥러닝에도 필요한 기본적인 내용들에 대해 다시 한번 짚고 넘어가도록 하자.

 

# 퍼셉트론

 신경세포뉴런과 비슷하게 입력 받은 데이터를 이용하여 선형 방정식을 통해 값을 계산하고, 계단 함수를 이용해 그 값이 임계치 이상이면 참, 미만이라면 거짓을 반환하는 것을 '퍼셉트론' 이라고 한다!

$ 진행 과정

1. 입력 신호가 들어오면 가중치(w)를 곱하여 가중합(z)를 계산한다.

2.  z값이 양수라면 참, 아니라면 거짓을 반환한다.

3. 계단함수를 통과한 값을 토대로 역전파 알고리즘을 이용하여 가중치와 bias를 업데이트한다. 

 

아래의 사진은 3번 과정에 해당한다.

 

퍼셉트론은 가중치의 업데이트가 계단함수 통과 후에 일어난다. 계단함수를 통과한 값은 1 or -1이므로 연속적인 Loss function을 사용하지 못한다. 이를 개선한 것이 바로 아달린이다.

 

 아달린에 활성화 함수를 추가한 것이 로지스틱 회귀이다! 활성화 함수에 대해서는 뒤에서 자세히...

---

# 활성화 함수와 손실 함수

 

1. 활성화 함수(Activation function)

 위의 사진들이 우리가 주로 사용하는 활성화 함수들이다. 각 함수가 어떻게 쓰이는지에 대해서는 머신러닝 시간에 이미 충분히 학습했으니 지금은 간단하게 각 함수의 단점을 이야기해보자.

sigmoid, Hyperbolic tanh 함수의 경우 기울기 손실 문제가 존재한다. 기울기가 손실되면 Loss를 업데이트 하지 못하기 때문에 큰 문제이다. 이는 ReLU를 사용하여 해결이 가능하다. 하지만 ReLU는 음수 값을 입력 받으면 항상 0을 출력하기 때문에 학습 능력이 감소하는데 이를 해결하기 위해 Reaky ReLU를 사용한다.

 

 

 

Q. 그렇다면 활성화 함수는 대체 왜 쓰는 걸까? 

 

 A. 위의 XOR의 경우를 예시로 보자. 선형적인 방식으로 이들을 나눌 수 있을까? 불가능하다. 따라서 활성화 함수는 선형인 데이터가 아닌 비선형 데이터를 다루기 위해서 사용한다! 여기에 더해 다양한 패턴 학습 기능을 위해서, 경사하강법을 효율적으로 하기 위해서도 사용한다! 

 

 

 

2. 손실 함수(Loss function)

 경사하강법은 학습률과 손실함수의 순간 기울기를 이용하여 가중치를 업데이트한다. 즉, 미분의 기울기를 이용하여 오차를 비교하고 최소화하는 방향을 찾는 것이다. 이때 손실함수 학습을 통해 얻은 데이터의 추정치와 실제 데이터가 얼마나 차이나는가를  통해 오차를 구합니다. 아래는 손실함수의 종류들입니다.

---

 

 

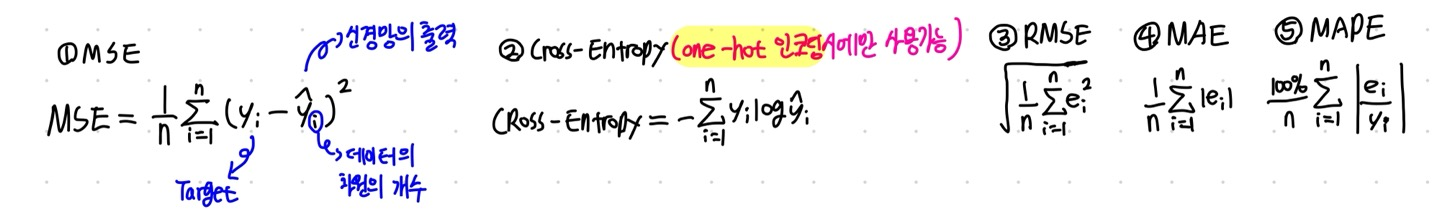
# 경사하강법(Gradient Descent)

함수 값이 낮아지는 방향으로 각 독립변수들의 값을 변형시키면서 함수가 최솟값을 갖도록 하는 독립변수의 값을 탐색하는 방법이다. 미분을 통해서 0이 되는 지점을 찾는 방법도 있지만 대부분은 복잡하고 비선형 패턴을 가져서 미분을 쓰기가 어렵다. 따라서 이때 사용하는 것이 바로 경사하강법이다! 추가로 경사하강법은 뒤에 딥러닝에서 배울 옵티마이저의 한 종류이다라는 것을 기억하고 있자.

 

 추가로 경사하강법에서 사용되는 몇가지 용어들을 정리해보자.

 

 

1. Batch : 모델이 가중치를 한 번 업데이트 시킬 때 사용하는 데이터들의 집합

2. Batch size : 모델의 가중치들을 한번 업데이트 시킬 때 사용하는 데이터의 개수

3. Epoch : 모델이 전체 데이터를 모두 사용하여 학습을 한 횟수

4. Iteration :  1 epoch에 필요한 batch의 개수

5. step : 한번에 이동하는 크기

6. Learning rate : 얼만큼 빠르게 이동하는가 

 

 

중요!

기울기에 대한 매개변수를 가지고 해당 손실함수의 최솟값이 존재하는지 보장할 수 없다. 그러나 해당 방향으로 손실함수의 값이 줄어드는건 확정적이므로 결론적인 최솟값을 찾기 위해서는 구한 기울기 정보로 나아갈 방향을 탐색해야한다!

 

 

 

 

$ 문제점

경사하강법에도 문제점이 존재한다! 이 문제점들이 발생하면 가중치를 업데이트 하지 못하고 결국 최적값을 찾지 못하게 된다.

 

1. Step 사이즈 설정

a. 너무 클 때 : 함수의 값이 커지는 방향으로 최적화가 진행될 수 있음

b. 너무 작을 때 : 최적의 x값을 찾는데 걸리는 시간이 오래 걸림

 

 

2. Local minima 문제

우리는 Global minimum을 찾아야 하지만, 경사하강법의 특성 상 시작 x값의 위치가 랜덤이므로 특정 경우 Local minima에 빠져 헤어나오지 못함

 

 

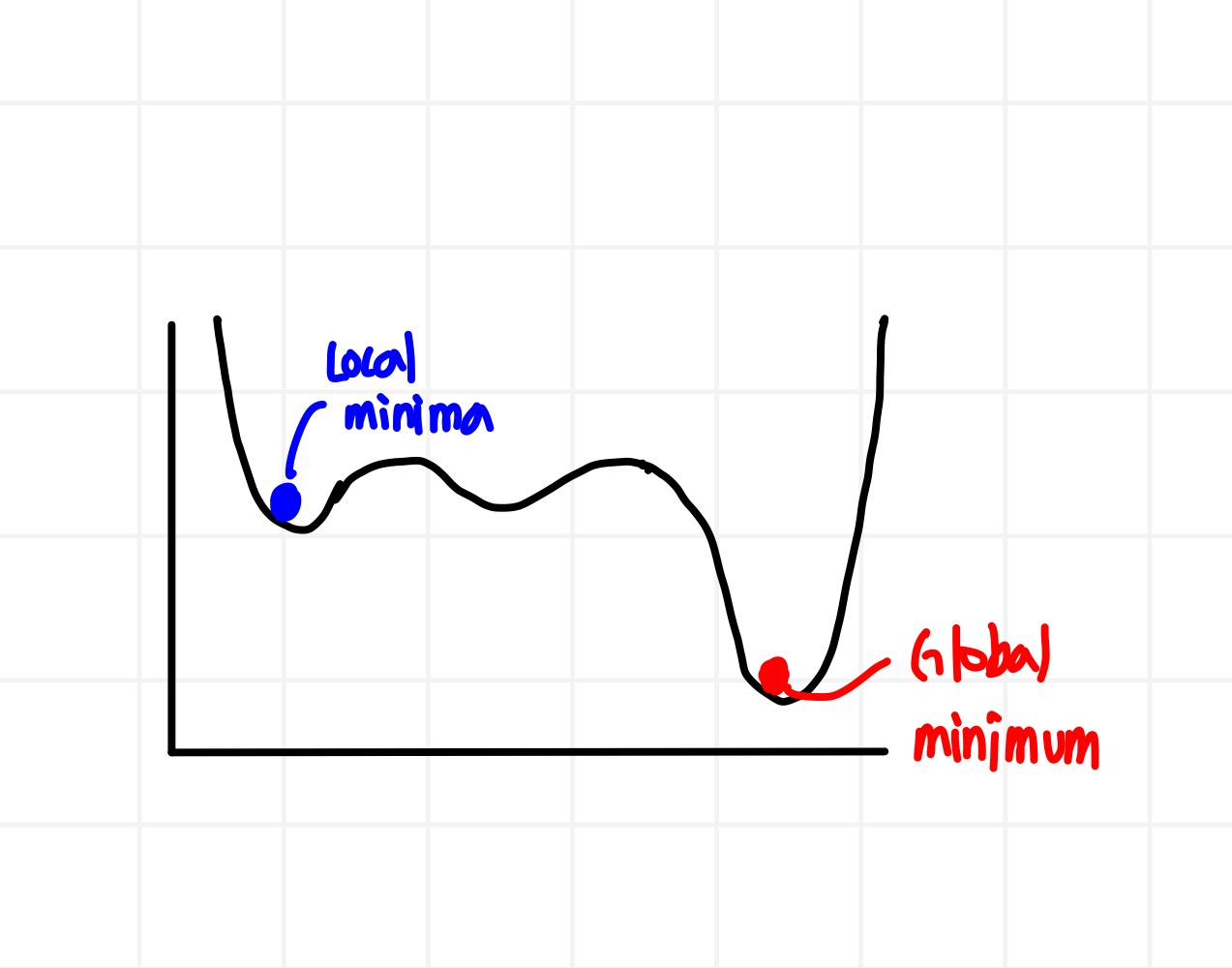
 3. Plateau 현상

평탄한 영역에 대해서는 기울기가 0에 수렴한다. 이런 지점에서 경사 하강법을 사용하면 결국 가중치가 업데이트되지 못하고 전역 최솟값을 갖는 지점이 아닌 점에서 정지할 수 있다. 이는 Local minima보다 자주 발생한다.

 

 

4. Oscillation 문제

경사하강법은 현재 위치에서 최적값 방향으로 수렴하는 것이 아닌 기울기에 따라 수렴한다. 만약 가중치들이 손실함수에 미치는 영향이 크게 상이하다면 그림처럼 크게 진동하여 최적값에 수렴하게 된다. 이를 oscillation이라고 한다. 진동폭이 크다는 것은 가중치가 불안정하게 수렴한다는 것이고, 이는 step의 크기가 크다면 최적값에 수렴하지 못하고 발산해버릴 수 있다. 따라서 가중치가 업데이트될 때 진동폭을 최대한 작게 만들어주는 것 또한 옵티마이저를 설정할 때 중요한 고려사항이다.

 

 

 

 SUMMARY...

결과적으로 우리가 궁극적으로 목표하는 것은 기울기 정보를 통해 기울기가 0이 되는 지점으로 나아가면서 가중치와 bias를 업데이트하면서 손실함수의 값이 최소가 되는 가중치와 bias값을 찾는 것입니다. 이러한 점을 잊지 않고 본격적으로 딥러닝으로 넘어가보도록 하겠습니다.