이 수업은 충남대학교 양희철 교수님의 기계학습을 토대로 작성한 글입니다
우리는 이전 시간에 선형회귀에 대해서 배웠다. 이번 시간에 배우는 내용도 로지스틱 회귀이다. 그렇다면 이들은 같은 회귀라고 생각해도 될까? 회귀의 값이 나오긴 하지만 회귀는 아니다. 왜냐하면 로지스틱 회귀는 분류 문제 해결을 위해서 사용하기 때문이다. 회귀로 나온 값을 어떻게 분류 문제에 사용할까?
이제 로지스틱 회귀에 대해 알아보자.
한마디로 정리하면... 선형회귀는 오차의 제곱 최소화, 로지스틱 회귀는 확률 분포를 최대화할 수 있는 모델링 분포!
1. Logistic Regression
# Odds

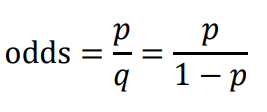
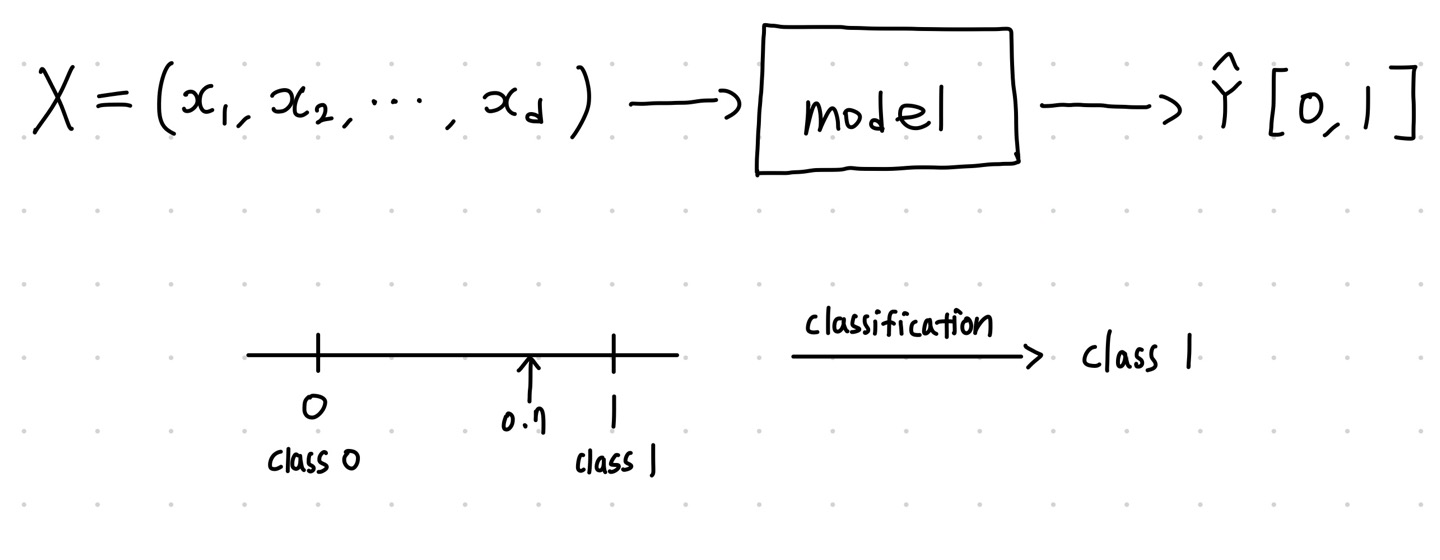
로지스틱 회귀는 회귀이기 때문에 y = B전치행렬X 꼴로 출력이 되는데 이 값은 연속적이다. 우리는 분류에 이용하기 위해서는 이를 discrete하게 나타내야 한다. 다시 말하자면, 연속적인 값을 갖게 하되, 해석을 확률로 하여 분류 문제를 푼다. 이를 위해 우리는 베르누이 분포와 odd라는 개념을 사용할 것이다. odd라는 것은 어떤 클래스에 속할 확률의 비, 클래스 p에 속할 확률 / 클래스 p에 속하지 않을 확률이다. 예시를 한번 보자.
EX)
● 게임에서 이길 확률 : 3/7
● 게임에서 질 확률 : 4/7
● odds = 3/7 / 4/7 = 3/4
odd를 이용해서 분류 문제를 해결할 수 있을 것 같다. 그런데 odd가 가지는 큰 문제점이 하나 있다
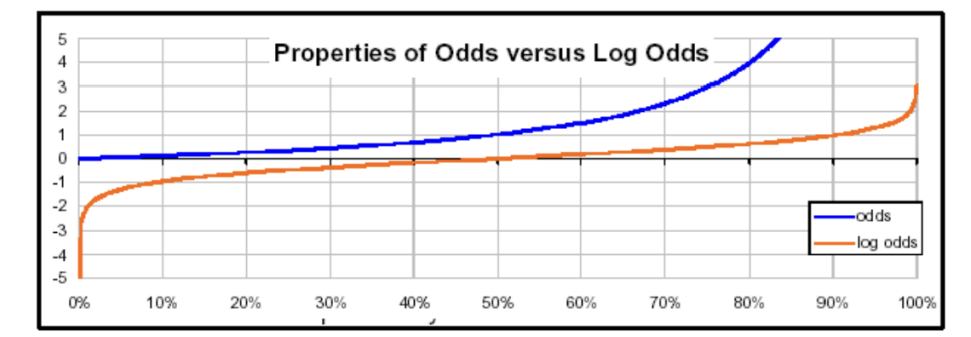
odd는 어떤 확률에 대한 값을 봤을 때, 모델의 출력을 확률로 하다보니 각각의 클래스에 대칭적이지 않다. 또한 odd의 범위는 0 ~ 무한대까지 가능하다.
=> 이를 보완하기 위해 우리는 대칭적이고 범위가 -무한대~무한대 사이인 Log odd를 사용한다!
# Log odds
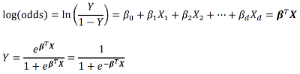

이 식을 보면 로지스틱 회귀의 결과는 log odd라는 것을 알 수 있다. log odds = B전치행렬X, 이 값을 Y에 대해서 정리하면 저런 식을 얻을 수 있는데 이 식이 바로 시그모이드 함수이다. 즉 이 함수를 통해 연속적인 값 BTX를 대입하면 클래스에 속할 확률을 얻어낼 수 있다.
아래에 식의 유도과정을 남겨놓았다.

# 선형 회귀 vs 로지스틱 회귀
● 선형 회귀 : 출력 값에 제한이 없고 연속적인 값을 출력한다.
● 로지스틱 회귀 : 출력 값의 범위가 0 ~ 1이고 로그 오드를 활성화 함수에 넣어서 클래스에 속할 확률로 계산하여 이산적인 값을 얻는다!
=> 가장 결정적인 차이는 X에 따른 Y의 변화를 해석할 수 있느냐 없느냐 이다. 선형 회귀는 해석이 용이하지만 로지스틱 회귀는 변화를 해석하기 어렵다. 이 부분을 예시로 한번 보자.
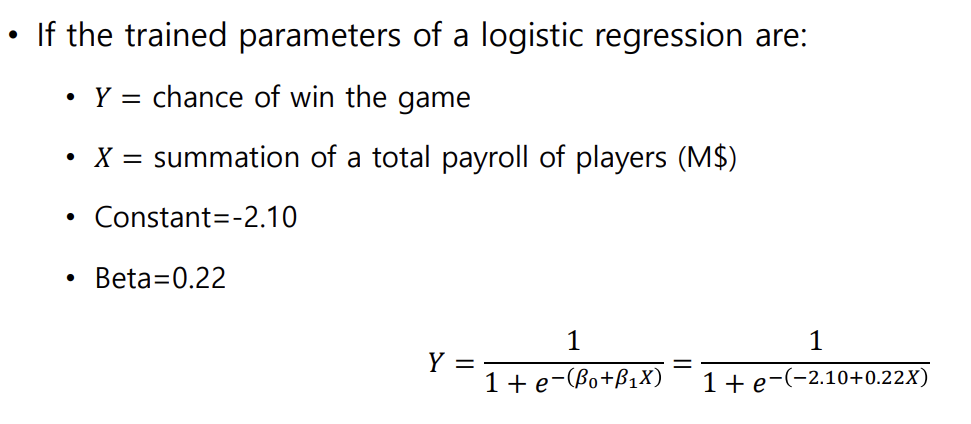

B전치행렬X = 2.10 + 0.22X = log odd , 이 식을 보면 X가 1 증가할 때는 B전치행렬X가 0.22씩 커진다. 즉, log odd는 0.22 커지고 odd는 e^0.22만큼 커진다. P를 직접 증가시키는 것이 아니라 odd를 증가시키는 것이기 때문에 직접적인 해석이 불가능하다!!
지금까지는 클래스 두개인 경우로만 보있다. 그렇다면 다중 클래스일 경우는 어떻게 해야할까?
2. Softmax Regression
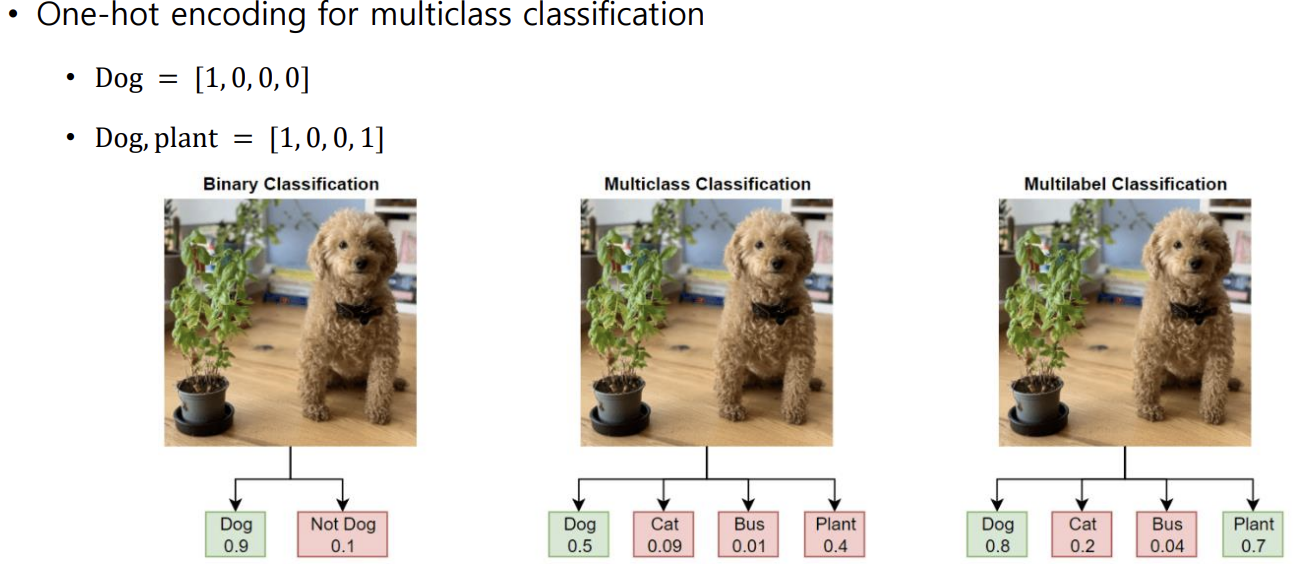
값을 라벨링해줘서 사용한다. 그런데 라벨링을 0,1,2,3...처럼 해주면 클래스 간의 거리가 달라서 문제가 발생한다. 왜냐하면 클래스가 독립적이기 위해서는 거리가 같아야하기 때문이다!!
=> 그래서 우리가 one-hot encoding을 사용한다. ex)1000 0100 0010 0001 거리가 전부 1이다.
따라서 타깃 값이 [1 0 0 0] [0 1 0 0] 이런 식으로 나오게 하는 것이 바로 Softmax function이다!
ex) [0.7 0.2 0.1] → [1 0 0]
Softmax Regression도 식으로 나타낼 수 있다
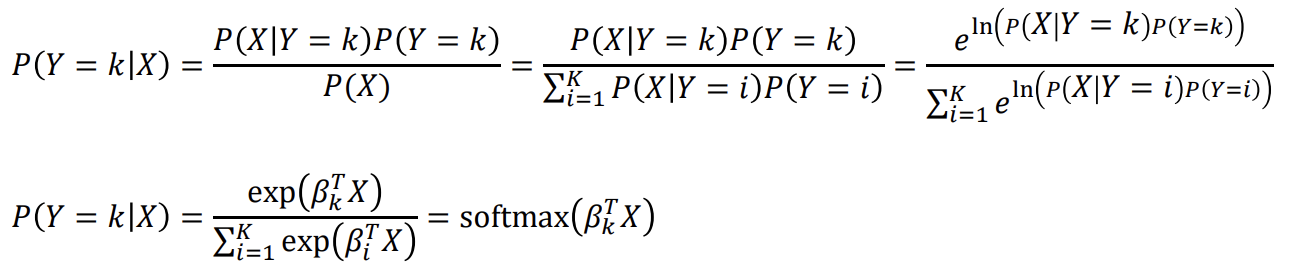
식을 보면 우리가 알던 분류의 확률식에서 다중 클래스이므로 exp와 ln을 취하는 것을 볼 수 있는데 이는 그래프의 형태가 시그모이드 함수의 장점이기 때문이다. 구체적으로 class가 나뉘는 점을 기준으로 기울기가 급격히 변해서 step function형태가 된다. 이 형태는 미분이 불가능하므로 ln과 e를 통해 미분이 가능한 함수의 형태로 만들어 준다!
우리가 궁극적으로 추구하는 목적은 분류가 얼마나 잘 되는가, 즉 손실이 적어야 한다는 것이다. 이를 나타내는 함수에 대해 알아보자
3. Cost Function


cost라고도 하고 Loss라고도 한다. 이를 사용하는 이유는 미분이 불가능하기 때문이다. 위에 주어진 식을 보면 알 수 있듯이 잘못된 class에 대해 h(x) 값이 1에 가까워지면 Loss가 커진다! 이진 분류에서 우리는 cross-Entropy 라는 손실함수를 사용한다. 다중분류도 쓰는 함수만 다를 뿐 방식은 같다. 따라서 시작점을 잡고 어느 방향으로 가는지 찾고 최적의 포인트, loss가 최소가 되는 지점을 찾는 과정을 거치는 것이 핵심이다.
아래의 구하는 예시를 보자.

우리는 분류에서 정확도를 기준으로 성능을 평가한다. 그런데 각각 어떤 상황에 쳐해 있느냐에 따라서 상황의 판단 가치가 달라진다. 이런 경우는 어떻게 해야할까?
4. Confusion matrix and ROC Curve
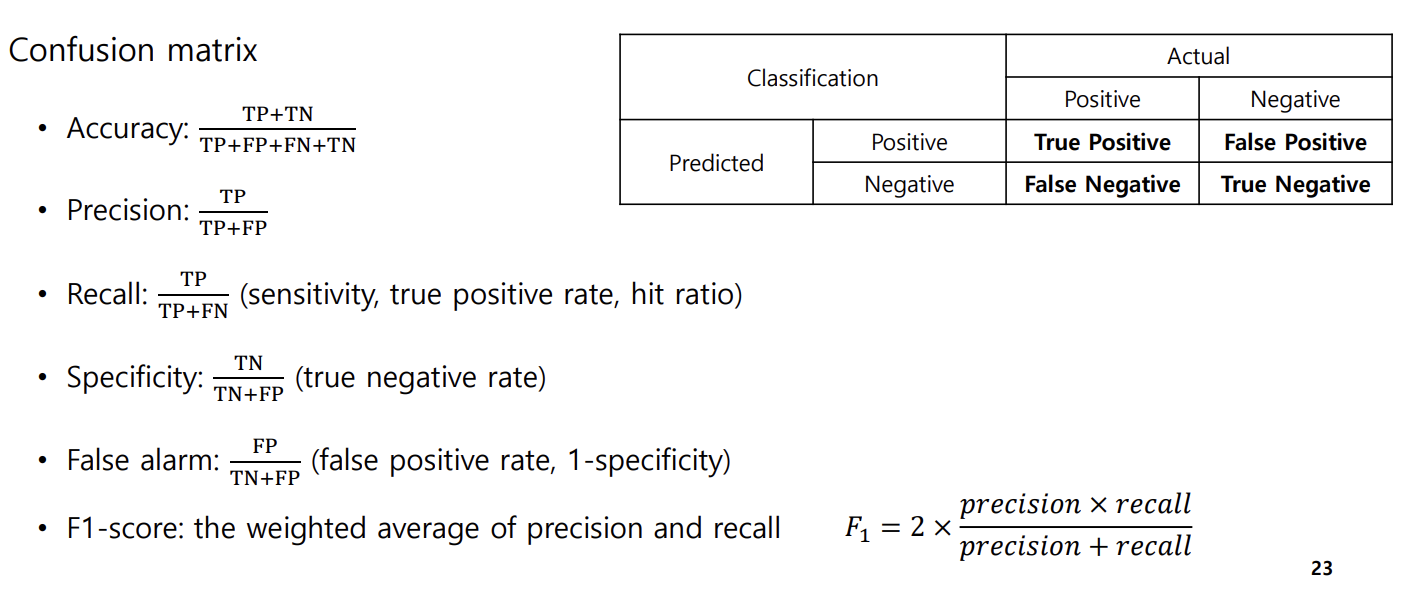
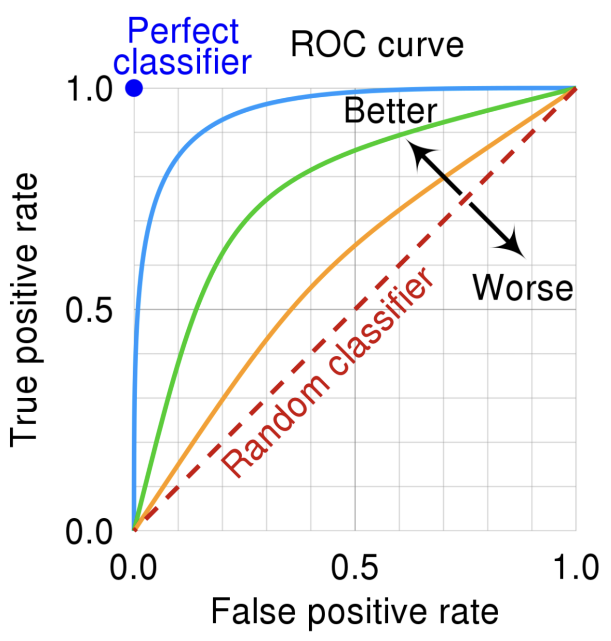
confusion matrix는 분류하는 상황의 판단 가치 차이, imbalanced-dataset 문제를 해결한다. ROC 커브는 분류의 결과가 아닌 출력의 형태가 얼마나 적절한가를 판단하기 위해서 사용한다. 즉 분류 기준(threshold)를 옮겨보며 잘못 분류되는 클래스의 비율을 확인한다는 것이다.
컨퓨전 매트릭스에서 ROC 커브를 그릴 때 사용하는 값은 두 개이다.
● Recall(True positive rate)
● False-alarm(False positive rate)
=> 커브의 안쪽 면적이 커질 수록 좋은 분류 기준이 된다! 아래에 예시 하나를 보자

결국 좋은 분류 기준이 되려면 true positive rate가 커야하고 false positive rage가 작아야 한다는 것을 알 수 있다.
다음 시간엔 K-nn에 대해서 알아보자
'AI > MachineLearning' 카테고리의 다른 글
| [ML] Decision Tree (0) | 2024.11.07 |
|---|---|
| [ML] Nearest Neighbor Method (0) | 2024.11.06 |
| [ML] Linear Regression (0) | 2024.11.04 |
| [ML] Bayesian Classifier (3) | 2024.11.04 |
| [ML] About Machine Learning (5) | 2024.10.21 |
